개요
프로젝트 기간
2025.07.16 ~ 2025.07.18
목적
Root-Raised-Cosine 필터 RTL 설계 · 타이밍 검증 · Welch PSD 평가
- 1. floating-point -> fixed-point modeling
- 2. RTL 설계 후, 입력(테스트) 벡터로 기능 검증
- 3. MATLAB을 통한 Welch PSD로 주파수 특성 검증
개발 환경
- 사용 언어 : Verilog, Systemverilog, MATLAB
- Tool : VCS, Verdi
- editor : vi editor
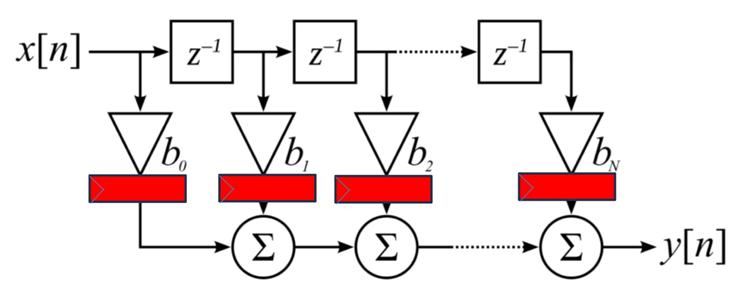
RRC Filter 핵심 원리
개념
디지털 통신 시스템에서 심볼 간 간섭 (ISI)을 최소화하고 신호의 전송 대역폭을 효율적으로 사용하기 위해 활용되는 펄스 성형 필터
주요 특징
- 심볼 간 간섭(ISI) 감소 : 신호의 꼬리 부분을 줄여 서로 섞이는 현상을 감소시켜 신호의 정확성을 높임.
- 펄스 성형 (Pulse Shaping) : 디지털 통신에서 비트를 심볼로 변환한 후, 효율적인 전송을 위해 신호의 모양을 최적화하는 펄스 성형 과정에 사용.
- 수신부 처리 : 송신부에서 RRC filter를 통과한 신호는 수신부에서 다시 RRC 필터를 통과하여 원래의 신호 파형으로 복원.
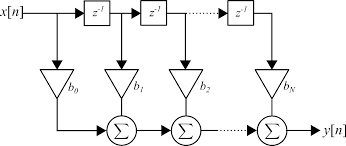
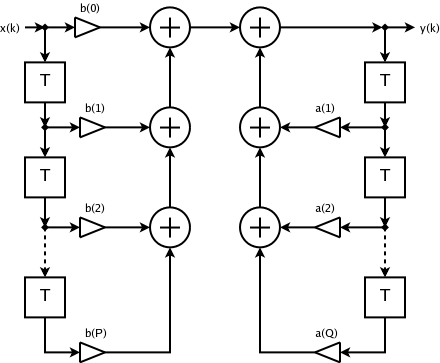
FIR vs IIR (구현 구조)
| 항목 | FIR (Finite Impulse Response) | IIR (Infinite Impulse Response) |
|---|---|---|
| 구조 | 피드백 없음(비재귀), 유한 탭 | 피드백 있음(재귀), 무한 임펄스 응답 |
| 위상 | 선형 위상 용이(대칭 계수) | 일반적으로 비선형 위상 |
| 안정성 | 항상 안정 (피드백 없음) | 극(pole) 배치에 따라 불안정 가능 → 설계/양자화 민감 |
| 차수 대비 응답 | 급경사/좁은 전이대역엔 탭 수 요구↑ | 낮은 차수로도 급경사 구현 가능(효율↑) |
| 지연 | 그룹지연 일정 = (탭수−1)/2 | 주파수 의존적인 그룹지연(왜곡 가능) |
| 고정소수점 | 양자화/스케일링에 비교적 강함 | 피드백 경로로 민감, 오버플로/발산 주의 |
왜 RRC는 FIR로 구현할까?
- 선형 위상으로 심볼 샘플 시점의 위상 왜곡 최소화
- 심볼 간섭(ISI) 억제에 맞는 모양을 탭 계수로 정확히 만들기 쉬움
- 항상 안정 + 고정소수점/FPGA 구현 시 예측 가능
- 폴리페이즈 구조와 결합해 업/다운샘플링 연산 효율↑
상세 설계
Fixed Point 모델링
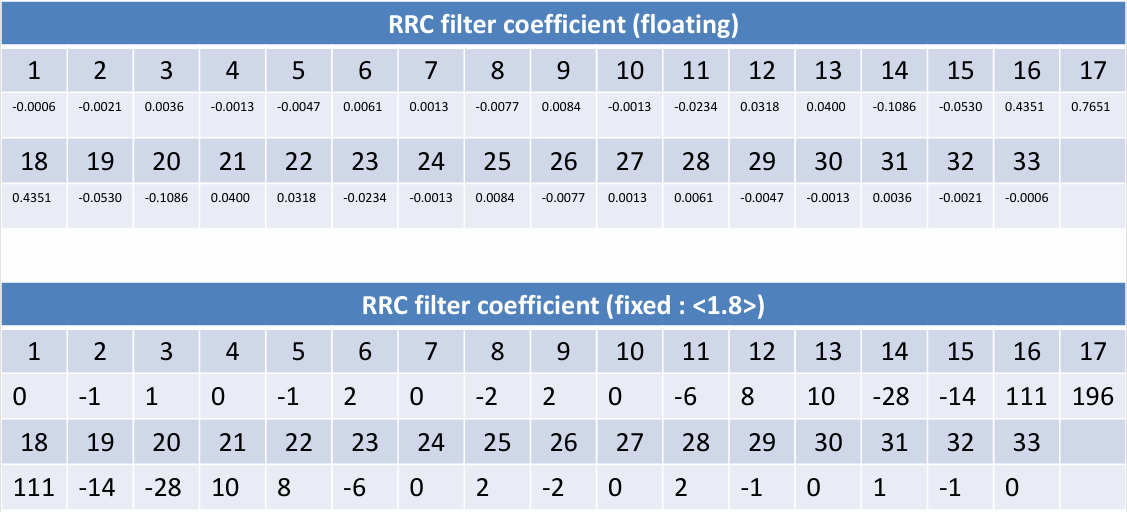
Timing 만족을 위한 Pipe 방식 설계 (개선 버전)
시뮬레이션 및 검증
Timingdiagram
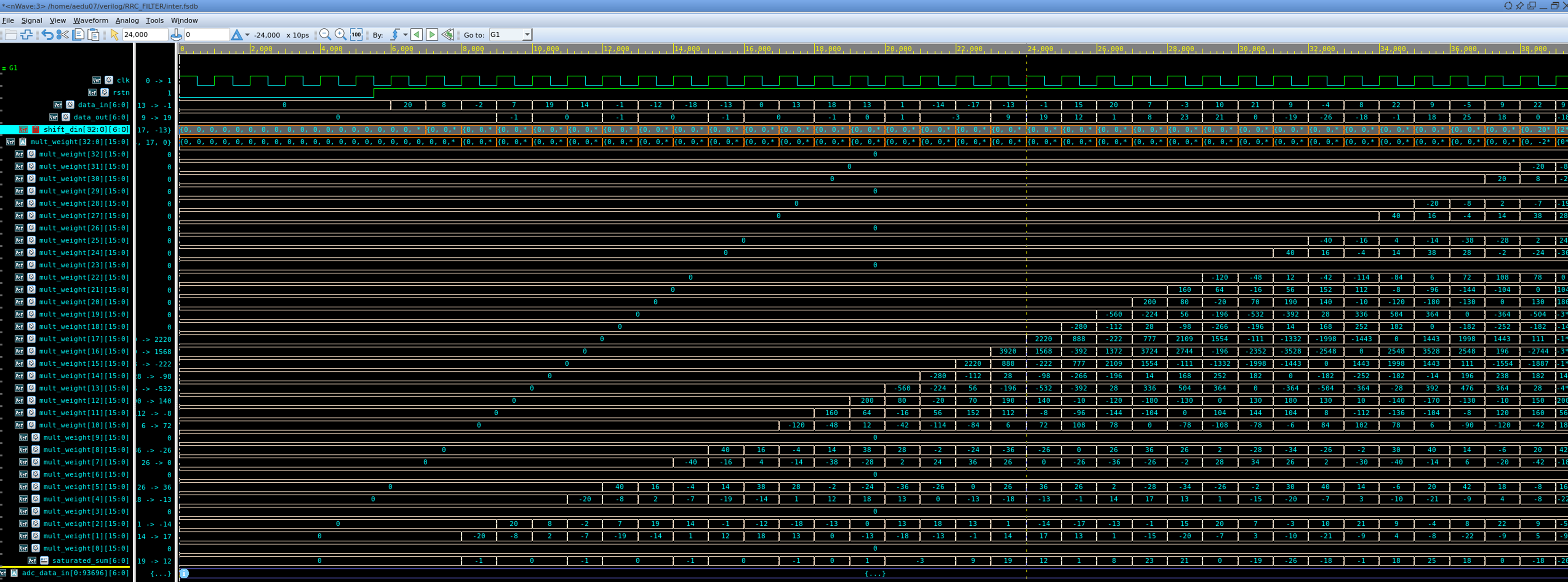
입력(테스트) 벡터를 통한 검증
// Input vector test
initial begin
fd_adc_di = $fopen("./rrc_din.txt", "r");
fd_rrc_do = $fopen("./rrc_dout_rtl.txt", "w");
i = 0;
while (!$feof(fd_adc_di)) begin
void($fscanf(fd_adc_di, "%d\n", data));
adc_data_in[i] = data;
//adc_data_in[i] = $signed(data[6:0]);
i = i + 1;
end
#800000 $finish;
$fclose(fd_rrc_do);
end
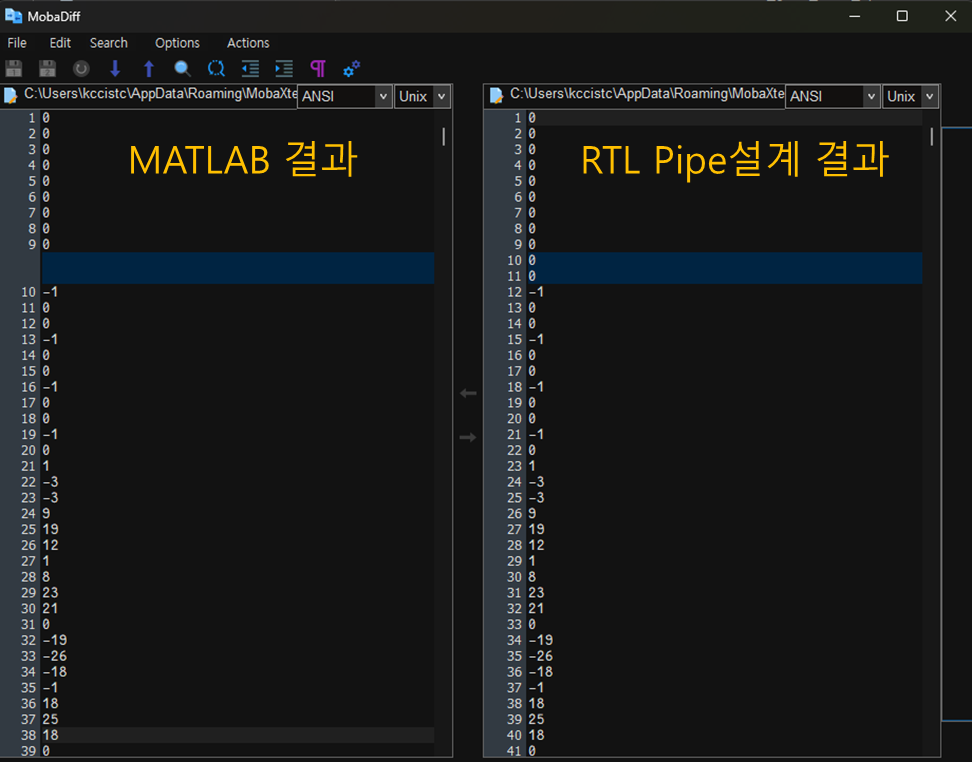
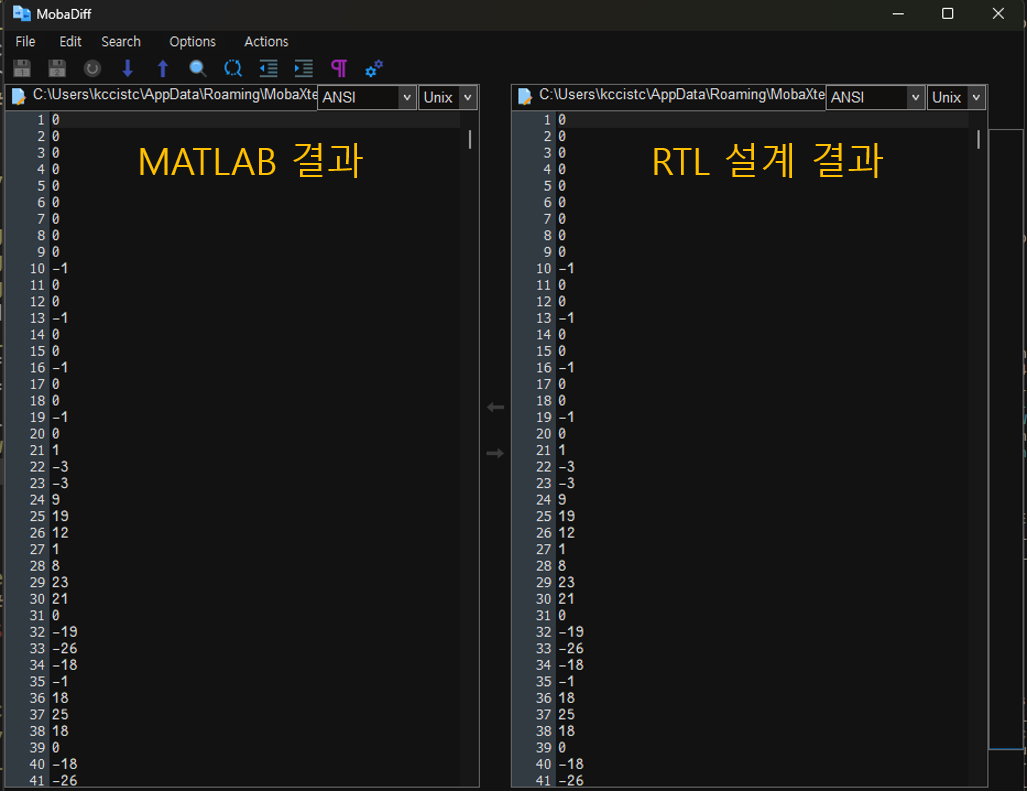
입력 벡터에 따른 출력 벡터 확인 -> MATLAB결과와 RTL 시뮬레이션 결과가 일치하는 것을 확인
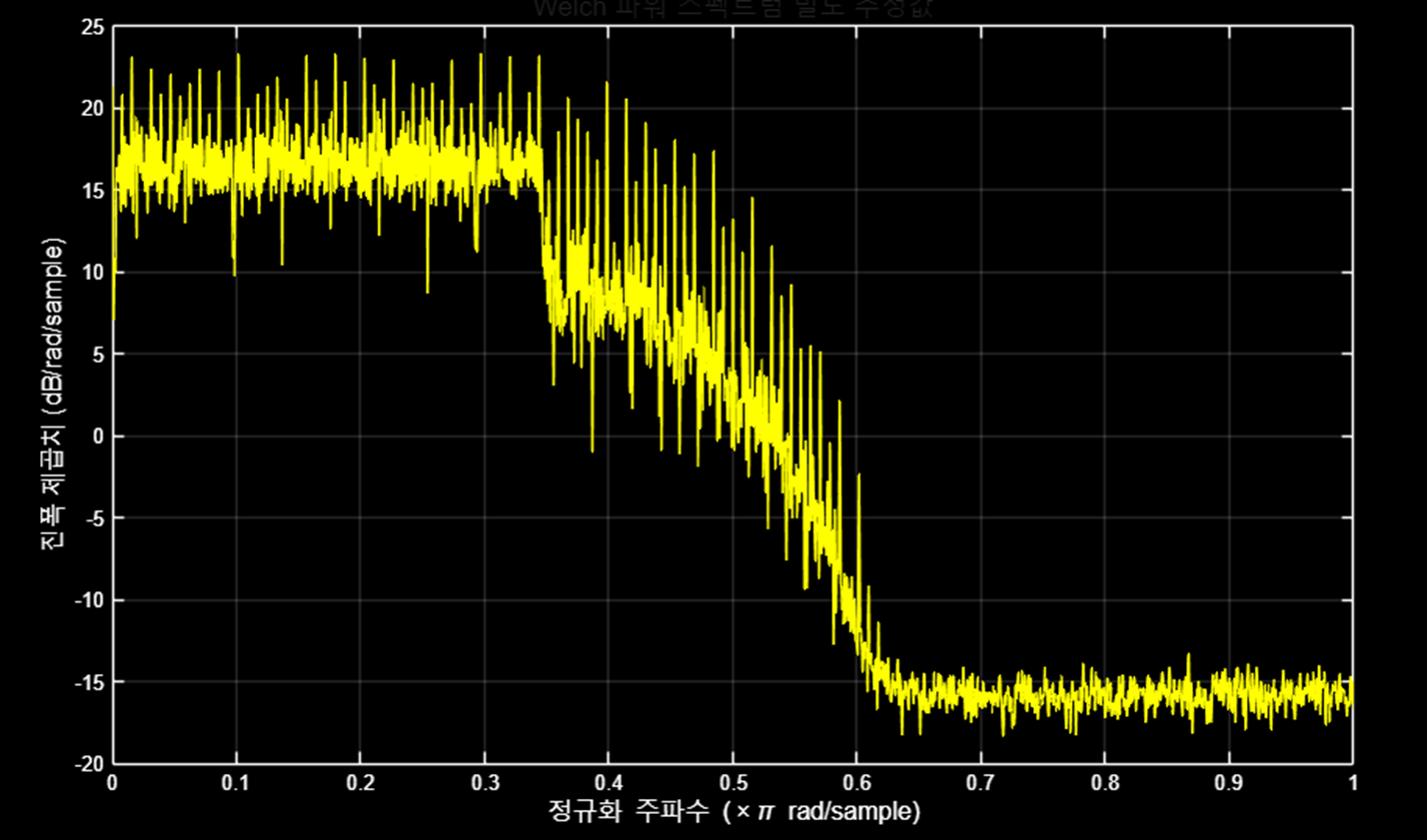
RRC 필터(고정소수점 RTL) 출력의 Welch 파워 스펙트럼 결과
트러블 슈팅
1. 문제 상황 : Setup Timing Violation
Synthesis 결과 Setup timing violation이 발생
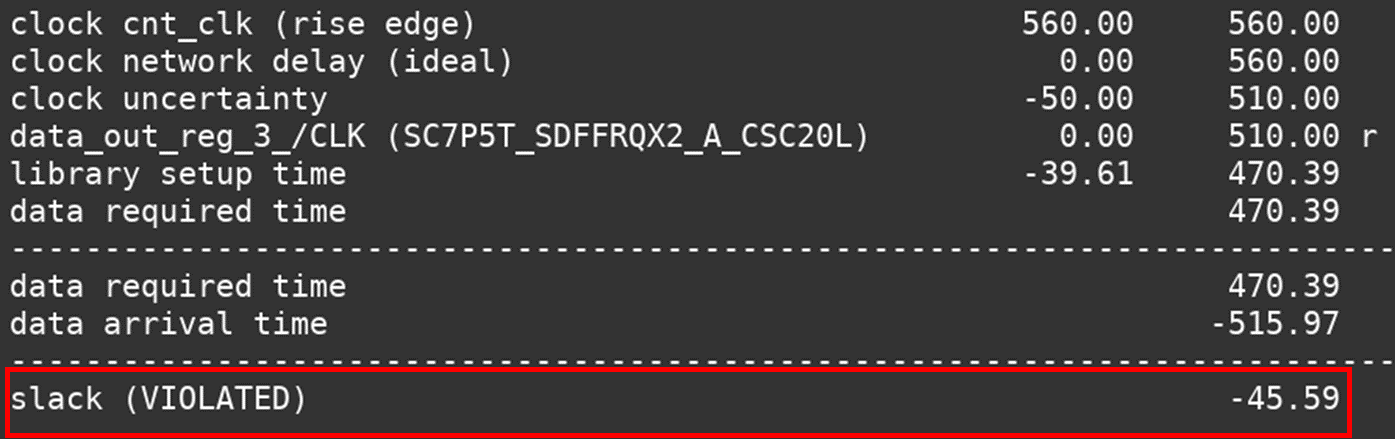
2. 원인 분석 : 곱셈과 덧셈 delay가 합쳐져 클럭 주기보다 path가 길어짐.
// 기존 설계
always @(*) begin
for (i = 32; i >= 0; i = i - 1 ) begin
mult_weight[i] = shift_din[i] * coeff(i);
end
sum = 0;
for (i = 0; i <= 32; i = i + 1)
sum = sum + mult_weight[i];
sum = sum >>> 8;
end
3. 해결 방법 : 2단 파이프 레지스터 삽입.
// Stage 1 (Multiply stage): RRC Filter의 계수를 곱해준 값을 저장.
always @(posedge clk or negedge rstn) begin
if (~rstn) begin
for (i = 32; i >= 0; i = i - 1) begin
mult_weight[i] <= 0;
end
end else begin
for (i = 32; i >= 0; i = i - 1) begin
mult_weight[i] <= shift_din[i] * coeff(i);
end
end
end
// Stage 2 (Partial sums): 33개의 덧셈을 8개씩 묶어서 부분합 4개를 저장.
always @(posedge clk or negedge rstn) begin
if (~rstn) begin
sum_p1 <= 0;
sum_p2 <= 0;
sum_p3 <= 0;
sum_p4 <= 0;
end else begin
sum_p1 <= mult_weight[0] + mult_weight[1] + mult_weight[2] + mult_weight[3] +
mult_weight[4] + mult_weight[5] + mult_weight[6] + mult_weight[7];
sum_p2 <= mult_weight[8] + mult_weight[9] + mult_weight[10] + mult_weight[11] +
mult_weight[12] + mult_weight[13] + mult_weight[14] + mult_weight[15];
sum_p3 <= mult_weight[16] + mult_weight[17] + mult_weight[18] + mult_weight[19] +
mult_weight[20] + mult_weight[21] + mult_weight[22] + mult_weight[23];
sum_p4 <= mult_weight[24] + mult_weight[25] + mult_weight[26] + mult_weight[27] +
mult_weight[28] + mult_weight[29] + mult_weight[30] + mult_weight[31];
end
end
assign total_sum = sum_p1 + sum_p2 + sum_p3 + sum_p4 + mult_weight[32];
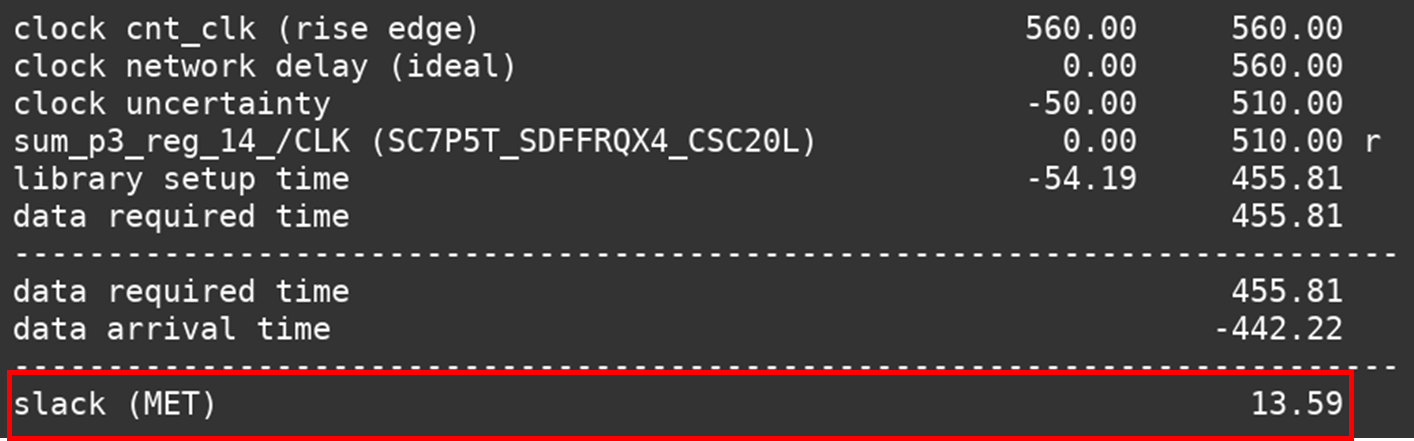
4. 해결 결과
느낀점
- 실수→정수(고정소수점) 감각: 비트 나누기(정수/소수), 반올림·포화 설정으로 모델과 하드웨어 결과를 맞추는 방법을 익힘.
- 타이밍=경로 쪼개기: 중간 레지스터(파이프라인)와 부분합으로 조합 경로를 짧게 만들어 타이밍을 만족시킴.